Since tiling patterns
, 
, 
, 
are orthogonal with each other,
perfect-magic squares can be obtained by
where 
and
Therefore, there are 
perfect-magic squares.
The possible combinations are given by
The number of independent perfect magic squares is given by
The factor 
comes from the definition in which
we take 
and its transposition 
is identical.
The factor 
appears, since
we take ,
and its rotations 
, 
, 
are identical.
Therefore, there exist three identical perfect-magic squares
which are
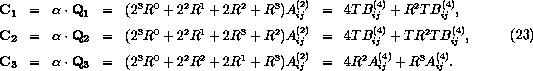
These perfect-magic squares correspond with those given by Grogono.