We have already obtained the two ideal tiling (6), (7)
of order N=4 without explanations in previous sections.
In order to confirm
whether or not the two are all of the possibly
independent tiling, we need to investigate the characteristic
of pair-symmetrical tiling.
Obviously, we can get the four different tiling patterns from
the ideal tiling (1) by the rotations R which are
, 
, 
and 
(see appendix.)
We will describe them shortly by
.
We adopt transposition T and rotation R as a symmetrical transformation
operators 
in (14).
Since 
, 
and 
, it is derived that
and 
.
Here we should note the transposition T does not satisfy the
association low with rotational operators. E.g.,
, but 
.
The operators satisfy the following operational table.
According to the table, we can categorize the 
pairs of tiling patterns into
{ 
, 
,
,
, 
,
, 
,
}
and { 
, 
,
, 
}, since
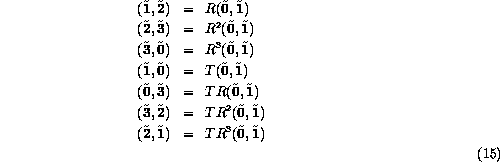
and
Simply, the above categories can be rewritten by
and
These patterns and
are not expressed by any symmetrical
transformation of each other. The symmetrical transformations
of these patterns cover all possible 12 pairs of pair-symmetrical
tiling patterns.
Therefore, the independent tiling patterns in N=4 are given by
and
based on conjecture 1 (in the case N=4, it is satisfiable theorem).
These tiling patterns correspond to 
, 
in
(11) and (12).
Since , are not
given by any (N-let-) symmetrical transformation of each other,
we call such independent tiling patterns "fundamental tilings".