
The problem is how we can cover the two dimensional plane with a set of numbers (0,1,...,N-1) so as to satisfy some symmetry. If we require the symmetry ``sum of any neighbor row, column or diagonal pair is the same value 1'' as long as possible, we can find the following tiling pattern by the binary digit set (0, 1).
With regarding the rotated or transposed patterns in the same light as the original tiling pattern (1), we can express as follows the patterns of choice which define the symmetry.
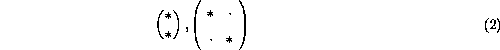
We call such patterns (configurations) of choice as ``N-lets'' hereafter. N-let choice can be applied either on any site or any orientation of the two dimensional tiling (1).
In (1), we compromise to have unsatisfiable cases
in which the row direction and diagonal direction do not satisfy
the symmetry with the probability ![]() .
.
How can we extend the tiling problem toward set of digits (0,1,...N-1) in base N? To answer this question, we would need to define symmetries in each order N as well as in the case of N=2.